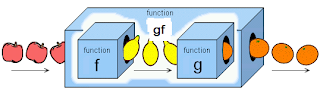
The diagram is a good illustration of a composite function.1. A set of values (Domain of f, apples in the diagram) are imput in the the f function box and the output will be the range of f.
2. The output from f (the lemon in the diagram) is again input into the g funtion box and the outcome will the range of this composite function gf.
3. Imagine that if some of the lemons out from f are too big to fit into g, then the composite machine will fail. Hence, we say that the range of f must be a subset of (including equal to) the domain of g for the composite function to exist.
Hence for composite function, there are a few points to take note of :
- The domain of gf is the domain of f.
- For gf to exist, range of f must be a subset of (including equal to) the domain of g.
- If gf does not exist, in order to make it exist, we have to narrow down the range of f (so as to make it a subset (or equal to) of the domain of g), and hence we need to narrow down the domain of f.
- The largest possible range of f that we can take is equal to the domain of g. Based on this largest possible range of f, we can find the corresponding largest possible domain of f.
Remark: Graph will be very useful in terms of finding range and domain!
Now you can do all the tutorial questions.
No comments:
Post a Comment