Complex Numbers: Lecture 1

Computation of complex numbers

• \[i^{2}=-1\]
• Real number is a subset of complex number.
• The representation of a complex number, z=x+yi is known as the cartesian form.
• Learn how to add, subtract and multiply two complex numbers
• Learn how to find the square root of a complex number.

Argand diagram

• We use the number line to represent real number, which is one dimensional. We use a plane to represent complex numbers, which has both real and imaginary part and hence two dimensional.
• Every complex number corresponds to a point on the plane and hence correspond to the position vector of that point.

Complex Numbers: Why do we need them?

I guess a lot of you are wondering why we need complex number. Can't we do with just real numbers? The following are videos that explain why we need complex numbers. I find it pretty good. =)


Part 1
http://www.youtube.com/watch?v=BDIv7r-X2kk


Part 2
http://www.youtube.com/watch?v=rBOzwh5-iGc&feature=related

Functions: Lecture 3

The diagram is a good illustration of a composite function.

1. A set of values (Domain of f, apples in the diagram) are imput in the the f function box and the output will be the range of f.

2. The output from f (the lemon in the diagram) is again input into the g funtion box and the outcome will the range of this composite function gf.

3. Imagine that if some of the lemons out from f are too big to fit into g, then the composite machine will fail. Hence, we say that the range of f must be a subset of (including equal to) the domain of g for the composite function to exist.

Hence for composite function, there are a few points to take note of :

• The domain of gf is the domain of f.
• For gf to exist, range of f must be a subset of (including equal to) the domain of g.
• If gf does not exist, in order to make it exist, we have to narrow down the range of f (so as to make it a subset (or equal to) of the domain of g), and hence we need to narrow down the domain of f.
• The largest possible range of f that we can take is equal to the domain of g. Based on this largest possible range of f, we can find the corresponding largest possible domain of f.

Remark: Graph will be very useful in terms of finding range and domain!

Now you can do all the tutorial questions.

Functions: Lecture 2

One to One Function

• A function is one-to-one if no two elements in X are mapped to the same values.
• You can use a horizontal line test to check whether a function is one-to-one.

Inverse Function

• A function has inverse if and only if it is one-to-one. (Why?)
• The domain of function f is the range of its inverse. The range of function f is the domain of its inverse. (Why?)
• The graph of a function and its inverse are the reflections of each other along the line y=x (Why?)
• To find the value for which \[f(x)=f^{-1}(x)\], you need to find the intersection between the graph y=f(x) and y=x using G.C. (Why?)

Inverse Trigonometry Functions

• To ensure sin, cosine and tangent functions have inverse, we have to define principle range (restrict their domains)
• Principal range of sin inverse is [ -pi/2, pi/2]
• Principal range of cos inverse is [0, pi]
• Principal range of tan inverse is [-pi/2, pi/2]

G.C.

When you plot the graph of a function in G.C., do you know how to input the domain like (-1,1)

Ans: You input x>-1 and x<1>"and" can be found in 2nd -> Math -> Logic

Tutorial Questions to attempt

You can attend Q2 to Q5 after today's lecture.

Function: Lecture 1

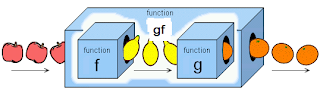
By the end of the lecture, you are supposed to know the followings:

1. What is a function?

• Can you give a definition?
• Given a graph or an expression, do you know how to check whether it is a function?
• How do you know whether two functions are identical?

2. What are the domain and range of a function?Given a function, how can you find out the domain and the range?
3. What is a restriction of a function?
4. What is maximal domain and how to find out the maximal domain given the function?

Some learning points in this lecture

Notations:

[a, b] This is usually called a closed interval since both the end points a and b are included in the range.

(a, b) This is usually called an open interval since both the end points a and b are NOT included in the range.

[a, b) and (a, b] These two are called half-open-half-closed intervals.

Remark: If one end of the interval goes to infinity (either positive or negative), that end is always denoted with the open bracket ")" or "("

\[D_{f}\] denotes the domain of function f

\[R_{f}\] denotes the range of function f


Concepts

1. A function maps one element in X to one and ONLY one element in Y. But two different elements in X are allowed to be mapped to the same element in Y.
(Think about this point carefully! Can you give an example of the functions that map two different values of X to the same value of Y?)

2. Based on point 1, we can have vertical line test to check whether a graph is a function.

• If any vertical line cut the graph at only one point, it is a function. (one value of X to only one value of Y)
• If there exists a vertical line cutting the graph at more than one point, it is not a function. (one value of X to many values of Y)

3. Two functions are the same if and only if they have both the same rule and domain.

4. If the domain of a function is not specified, it is taken to be the maximal domain for which the function is defined, i.e. x takes whatever values that it is allowed to take.

G.C Skills

How to graph a function with the domain?

Remark: You have to take note of the END POINT in the graph to see whether it is included. The range can be read from the graph.

Tutorial question to attepmt

You can attempt Tutorial Q1 after today's lecture.

An Interesting function

In A level, you usually see functions that are very nice. Have you ever thought of a function like this:
\[f(x)=\left\{\begin{matrix}1 & \mbox{if x is rational}\\ 0 & \mbox{if x is irrational}\end{matrix}\right.\]

If you want to draw a graph of the function, remember that
1. Between every pair of irrational numbers, there is a rational number.
2. Between every pair of rational numbers, there is a irrational number.

Have you thought of how to integrate such a function? Does it have an area between the graph and the x-axis?

The answer to the question reveals a very important relationship between the rational and irrational numbers.

Let's start the MATH journey 2010!

Hi all,

This is a blog to assist you in the learning of H2 math in 2010. The content of this blog includes the following:

1. A summary for the lecture after each lecture.

2. The tutorial questions that you can attempt after each lecture.

3. interesting historical stories or video regarding the topics that you are learning

You are welcome to ask questions in the comments. I will answer them during the tutorial.

This blog is intended to help you to become more independent and active in the learning process. I hope you will make full use of it.

Sincerely hope that the case in the picture won't happen in my class =P