revision: complex number

Revision: Binomial, Poisson and Normal distribution

revision: integration

Revision: Differentiation

Lecture 4: Normal distribution

In today's lecture, we learnt two approximations.

1. Binomial distribution to normal distribution

If X~B(n, p)

• Recall that if when n is large, and np is smaller than 5, we can approximate X to Poisson distribution with mean np, i.e. X~Po(np)
• If n is large, np is larger than 5 and n(1-p) is also larger than 5, we can approximate X to Normal distribution with mean np and variance np(1-p), i.e. X~N(np, np(1-p)

2. Poisson distribution to normal distribution

If \[X \sim Po(\lambda)\], and \[\lambda>5\],

we can approximate X to normal distribution, \[X \sim N(\lambda,\lambda)\]

Remark: Remember to do the continuity correction when you approximate either Binomial or Poisson distribution to Normal distribution.

You can attempt tutorial 15B now.

Lecture 3: Normal distribution

In today's lecture, we learnt three important properties of Normal distribution.

1. Sum of two independent normal random variables

2. Sum of n independent observations from the same Normal distribution

3. Multiple of Normal variables.

Remember the following rules:

• All the random variables must be independent.
• When two random variables are added or subtracted, their variance are always added.
• When a random variable is multiplied by a constant, say, a, the variance is multiplied by a^2.
• You can only add or multiply the variance, NOT the standard deviation.

Lecture 2: Normal distribution

In this lecture, you have learnt the following points:

1. the use of " invNorm"

Example: X~ N(17,11), P(X is smaller than a ) =0. 38, use invNorm (0.38, 17, sqrt(11)) to find the value of a.

Note: If the given information is P(X is bigger than a)=0.38, you have change it to P(X is smaller than a)=1-0.38=0.62 before you use the "invNorm" function.

2. Properties of Normal distribution

If \[X\sim N(\mu ,\sigma ^{2}) \], \[aX+b \sim N(a\mu+b, a^{2}\sigma^{2})\]

3. Standard Normal distribution

• Standard Normal distribution is the normal distribution with mean 0 and variance 1.
• We can change any normal distribution to standard normal distribution. \[X\sim N(\mu ,\sigma ^{2}) \], \[\frac{X-\mu}{\sigma}\sim N(0,1)\]

You can make use the properties of Normal distribution to prove it.

Binomial and Poisson distribution Lecture 5+ Normal distribution Lecture 1

1. Binomial and Poisson distribution

For binomial and poisson distribution, we learnt about the approximation binomial distribution to poisson distribution today.

If X~ B(n, p), with n is larger than 50, p is smaller than 0.1 with np smaller than 5, X~ Po(np) approximately.

2. Normal distribution

In today's lecture, we learnt a few things on Normal distribution.

• Continuous random variable

Normal distribution is for continuous random variables. ( Unlike Binomial and Poisson distributions, which are for discrete random variables. )

For a continuous random variable, there is a probability density function (pdf) f(x) associated with it.

However, f(a) does not denote the probability at a. Instead, for continuous random variable, the probability at any specific value is 0. We can only compute the probability of a certain interval, e.g. (a, b). The area under the curve of f(x) from a to b will give the probability P(x is between a and b )

• Important result for Expectation and variance

Expectation

E(a)=a

E(aX+b) = aE(X) + b

E(aX+bY)=aE(X)+bE(Y)

Variance

Var(a) = 0

Var(aX+b)=a^2 Var (X)

Var(aX+bY)= a^2 Var(X)+b^2 Var(Y) if X and Y are independent

• Normal distribution \[X\sim N(\mu, \sigma ^{2})\]

Normal distribution is symmetrical about the mean. The mean, median and mode are all equal.

When you use G.C. to evaluate normal distribution, you should key in:

normalcdf ( lower bound, upper bound, mean, standard deviation)

Lecture 4:Binomial and Poisson distribution

In this lecture we learnt two important ideas.

1. Find the mode for Poisson distribution

• Similar to Binomial distribution, the Poisson distribution has probabilities that increase to a certain level and decrease subsequently.
• Use G.C. to find the probabilities for each value of X and look for the one with highest probability.
• The mode is usually near the expectation.

2. Additive properties of Poisson Random variable

• If X~Po(a) and Y~Po(b) , where X and Y are independent, then

X+Y ~ Po (a+b)

After this lecture, you can attempt Q1,2,3,4 (except (v)) ,Q5, Q6, Q7.

Lecture 3:Binomial and Poisson distribution

In this lecture we focus on the following points:

1. What is the characteristics of a Poisson distribution?

2. What is the probability distribution function, expectation and variance of Poisson distribution?

What is the characteristics of a Poisson distribution?

• The rate of occurance is constant throughout the given time interval or given space.
• The event happens singly and randomly and it is rare event.
• The probability of two events happening at the same time is negligible.
• The events happening in different time intervals or space are independent.

Examples of Poisson distribution includes no. of defects, demand of a certain item, no. of telephone calls etc.

What is the probability distribution function, expectation and variance of Poisson distribution?

• The p.d.f. of Poisson distribution is \[P(X=r)=\frac{e^{-\lambda}\lambda^{r}}{r!}\] where r=0,1,2,3,... (up to infinity)
• Expectation and variance: \[E(X)=\lambda\] \[Var(X)=\lambda\]

You can attempt Q1 - 3 in the tutorial 14B.

Lecture 2: Binomial & Poisson Distribution

In this lecture, we learnt three concepts: expectation, variance and mode

Expectation is the mean (average) value of the random variable after a large number of trials.

Variance is about the spread of the data, i.e. the larger the variance, the more likely that you will get a outcome that is far away from the expectation.

Mode is the value that is most likely to occur.

To do a question in Binomial distribution, you have to take note of the following:

• define the random variable first
• check that it does follow Binomial distribution
• find out what is the value of n (no. of trials) and p (probability of success)
• understand what the question is asking about and use G.C. to solve the problem

You can attempt all the questions in tutorial 14A after this lecture.

For enrichment: \[E(X)=\sum_{k=1}^{n}P(X=X_{k})X_{k}\]

\[Var(X)=\frac{1}{n}\sum_{k=1}^{n}P(X=X_{k})(X_{k}-E(X))^{2}\]

Challenging question: For a game, you have a probability of 0.5 to win 2 dollars, 0.4 chances to win 3 dollars and 0.1 chances to win 10 dollars. If you need to pay 3.5 dollars to play the game, would you want to play?

Lecture 1: Binomial & Poisson Distribution

In today's lecture, you have to take note of the following points:

1. What is a random variable? What is probability distribution?

2. Under what condition will the random variable follow Binomial distribution?

3. What is the probability distribution function for Binomial distribution?

What is a random variable? What is probability distribution?

Two important characteristics of a random variables are reflected in its name. " Variable" tells us that it is a value that can change. "Random" tells us that the change of the value is random, i.e. there is no way to predict the value.

There are two types of random variables: discrete and continuous. If you can count the possible values taken by the random variable, it is discrete. Otherwise, it is continuous.

A random variable can take a certain set of possible values. For each of these value, there is a certain probability associated. The way that the probability is distributed among these possible values is called the probability distribution. It can be summarized in terms of a formula or in a table form, which is called the probability distribution function of the random variable.

Under what condition will the random variable follow Binomial distribution?

• There are n independent trials. (Independence means that the outcome of any trials will not affect the outcome of rest of the trials. )
• For each trial, there are two possible outcomes, one success and one failure.
• The probability of success is constant in each trial.

Remark: It is very important to know the condition for each type of distribution. It helps you to determine the right distribution to use when given a problem.

3. What is the probability distribution function for Binomial distribution?

There are two important values to take note of for each binomial distribution: the no. of trials, n, and the probability of success, p. If X~B(n, p)

\[P(X=r)=^{n}\textrm{C}_{r}p^{r}q^{n-r}\]

After this lecture, you can attempt Tutorial 14A Q1

Lecture 3: probability

In the last lecture on probability, there are two emphasis.

1. Mutually exclusive and independent events

2. Tree diagram

Mutually exclusive and independent events

It is important to differentiate these two types of events.

• Mutually exclusive events mean that they can never happen together.
• Independent events means that the happening of one event will not affect the probability of the other happening.
• Mutually exclusive events are NOT independent because if one event happens, the probability of the other happening drops to zero! (It does affect the probability of the other event happening.)
• It is very difficult to judge whether two events are independent based on your intuition. Please use the definition of independent events P( A intersect B) =P(A)P(B) to check whether two events are independent.

Tree diagram

• Tree diagrams are useful if

1. The event has a few stages

2. The outcome in one stage will affect the probability in the next stage.

By the end of the lecture, you can attempt tutorial 13.

Lecture 1&2: Probability

Probability is a study of random events and chances. The modern theory of probability is founded by two mathematicians, Pascal and Fermat during the seventeenth century and it was started by the study of the chance of winning in a gambler's game.

In these two lectures, you need to understand the first few concepts.

1. The meaning of the basic terms: experiment, outcome, sample space and event

2. Classical method of obtaining probability (Important concept!!!): the probability of an event equals to the no. of ways that the event can occur dividing the total number of possible outcomes.

Remark: Classical method is useful only if each outcome are equally likely to happen.

3. Venn Diagram: Learn how to draw the Venn diagram and derive the formula from the Venn diagram

4. Conditional probability (Extremely important!!!):

• Definition: P(A|B)=P(A intersect B)/P(B)
• To calculate conditional probability, please make use of the definition rather than depending on your intuition. Your intuition is not always correct!

Tips for questions on probability:

• identity and define the events first
• change all the statements in terms of probability
• summarize the information in the question before you start to do the question

You can attempt all the questions in tutorial 13 except Q3 and 4.

Probability: Interesting Puzzle

A gambler bets half the money in his pocket on the toss of a coin, winning an equal amount for a head and losing his money if the result is a tail. He repeats this many times, each time betting half the total money he has. After 2n plays he has won exactly n times. Has he more money, the same amount or less money than he started with?

Permutations and Combinations: Lecture 2

In this lecture, you learn about combinations.

1. Notation of combinations and what does it mean?

If you choose r objects from n distinct objects disregard of the order of choosing, the no. of combination is represented by \[_{}^{n}\textrm{C}_{r}\]

Do you realise that combination notation is also used in binomial expansion? Why is it so?


2. Relationship between permutation and combination

\[_{}^{n}\textrm{P}_{r}={}^{n}\textrm{C}_{r}\times r!\]

Permutation means that the order of choosing is important while for combination the order is not important. Hence, the no. of ways of permutation with r objects chosen from n distinct objects is equivalent of the no. of ways of choosing r objects disregard of the order multiply by the no. of ways to arrange the r objects in order.

After this lecture, you can do tutorial 12.

Permutations and Combinations: Lecture 1

In this lecture, we learn about the following concepts.

1. the addition and multiplication principle
2. permutations

• permutation with distinct objects
• permutation with identical objects
• permutation allowing repetition
• circular permutation

The addition and multiplication principle

• The addition principle is used in the case that you have a few different ways to complete a task.
• The multiplication principle is used in the case that you have different stages in a task and you have a few ways to complete each stage.

Permutation with distinct objects

• When you choose r objects from n distinct projects (the order of choosing matters), the no. of ways that you can do so is \[_{}^{n}\textrm{P}_{r}\]

In the another way, we can use the multiplication principle. To choose the first object, we have n choices , i.e. n no. of ways. To choose the second object, we are left with (n-1) choices, i.e. (n -1) ways. Hence, the no. of ways to choose r objects is n(n-1)(n-2)...(n-r+1)

• In the GC, you can find "nPr" in MATH -> PRB

Permutation with identical objects

• If we are to arrange r objects with r1 of type 1, r2 of type 2,... and rn of type n, where r1+r2+...rn=r, the no. of ways is given by r!/(r1!r2!...rn!)

• The rationale behind this formula:

r! is the no. of ways to arrange the objects if all of the objects are different. If some of them are identical, we actually overcount the no. of ways by a factor, which is the no. of ways we can arrange those identical objects.

Permutation allowing repetition

• If we choose r objects taken from n distinct objects in order, and each object can be used more than once, the no. of ways to do so is \[n^{r}\], since each time when we choose an object, we have n choices.

Circular permutation

• The no. of ways to arrange n distinct objects in a circle is (n-1)!
• The rationale behind the formula:

First of all, we can consider the permutation of n distinct objects, which is n!. However, when we arrange them in a circle, we found that some of the arrangement becomes identical. In fact, since we only care about the order in the clockwise manner and ignore the starting position, every identical arrange is repeated n times. Hence, in the end, the no. of different arrangement is n!/n, which is (n-1)!

Remark: circular permutation with identical objects do not have a general formula. You might want to think about the reason.

Differential Equation: Lecture 4

In today's lecture, we learnt more about the application of DE in real-life.

1. Radioactive decay (You need to understand the term "half life", which means the time taken for the material to distintegrate into half of its original amount. )

2. Newton's law of cooling (The rate of decreasing of a object's temperature is directly proportional to the temperature difference between the object and the surrounding. )

3. Change of volume with time.

For this type of questions, you can follow the steps below to solve the problem.

- Look for key phrases that gives you the differential equation, which is usually a statement on the "rate of increase/decrease".

- Form the DE and solve it to have a general solution. (A solution might have one or two unknown constants.)

-Look for other data given in the questions. Use these data to solve for the unknown constants in the previous step.

By now we have finished the chapter DE, you can attempt all the tutorial questions.

Differential Equation: Lecture 3

In lecture 3, you learnt about two main concepts.

1. What is the family of curves?

2. How to model a question using DE and solve the problem?

1. Family of curves

The general solution of a DE can be represented by a set of curves graphically ( one curve for each value of the arbitrary constant). This set of curve is called the family of solution curves of the DE.

A particular solution of the DE corresponds to one specific curve in the family.

When you are asked to sketch the family of curves, you usually choose C=-1, 0 and 1 unless otherwise specified by the question.

Please use G.C. to help you in the sketching!!!

2. Modelling using DE

DE can be used to model a lot of real-life problems including physical phenomenon, process, human behaviours and population growth.

To model a problem with DE, follow the steps below.

Step 1: look for phrases like " the rate of increasing/decreasing of ... is proportional to ..." or ".... is increasing/decreasing at the rate proportional to... "

These phrases give you the Differential Equation.

Step 2: Solve the DE, usually by direct integration. The solution usually has some unknown constants.

Step 3: Use the given data in the question to find out the unknown constants.

After lecture 3, you will be able to do the whole tut11b if you are good at modelling. However you might wanna attempt Q1, 2, 3 , 6 first since they are similar to what we have gone through in the lecture.

Differential Equation: Lecture 2

In lecture 2, we learnt two main skills.

1. How to solve a second order DE in the form of \[\frac{\mathrm{d^2}y }{\mathrm{d} x^2}=f(x)\]

2. How to use substitution to solve a first order DE that cannot be solved by direct integration.


1. How to solve a second order DE

Step 1: integrate both sides once to get a first order DE (the first order DE obtained will have one arbitrary constant.)

Step 2: integrate again to get the general solution. (the general solution will have 2 arbitrary constant.)

2. How to use substitution to solve a first order DE that cannot be solved by direct integration.

Step 1: differentiate the given formula for substitution. (e.g. z=1/y)

Step 2: replace the dy/dx in the original DE by dz/dx

Step 3: observe whether there are still y in the DE, replace the y using substition or other methods.

The final DE should be in term of x and z and should be solvable by direct integration.

Step 4: solve the DE to obtain a relation between x and z.

Step 5: replace z by y using the substition given in the question.

After lecture 2, you can do the whole tutorial 11a.

Differential Equations: Lecture 1

The term differential equation was coined by Leibniz in 1676 for a relationship between the two differentials dx and dy for the two variables x and y.

A differential equation is an equation which involves an unknown function (e.g. y) and some of its derivatives. Solving a differential equation (DE) is to find a relation between the variables, say y and x, that satisfies the DE.

In today's lecture, we have learnt the followings:

1. Terminology: what is the order and degree of a differential equation?

2. How to solve the following two types of DEs?

• \[\frac{\mathrm{d} y}{\mathrm{d} x}=f(x)\]

To get the solution, we use \[y=\int f(x) dx\]

• \[\frac{\mathrm{d} y}{\mathrm{d} x}=f(y)\]

To get the solution, we use \[\int \frac{1}{f(y)} dy=x\]

3. General solutions and particular solutions

A differential equation has infinite no. of solutions. For example, \[y=x^{2}+1,y=x^{2}+2 \] are both the solutions for the DE \[\frac{\mathrm{d} y}{\mathrm{d} x}=2x\]. Indeed, \[y=x^{2}+C\] will be a solution for the DE with any constant C.

In this case, we call \[y=x^{2}+C\] a general solution.

If a condition on x and y is given, say y=1 when x=0, then we can find out a specific value of C and that is a particular solution.

After today's lecture, you can attempt Q1-Q7 in tutorial 11a.

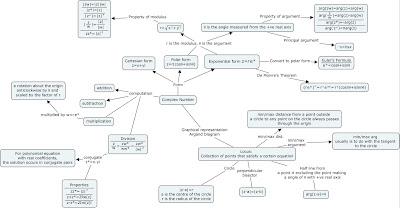
Complex numbers: Lecture 7

In this lecture you have learnt how to draw the loci in the form of \[arg(z-a)=\theta\]

Remember the description of such locus:

Let A and P be the points in the Argand diagram representing a and z respectively,

The locus is the half-line from A (excluding A) that makes an angle theta with the positive real axis.

In addition, we need to know the following geometrical knowledge:

1. Given a point A outside a circle with centre O, find a point B on the circle such that AB is longest.

Answer: B is the point such that AB passes through O.

2. Given a point A outside a circle with centre O, find a point B on the circle such that AB is shortest.

Answer: B is the point such that the extended AB passes through O.

3. Given a point A outside a circle with centre O, find a point B on the circle such that angle BAO is maximum.

Answer: B is the point such that AB is the tangent to the circle. (There are two such point B.)

This is the last lecture on complex numbers. Now you should finish the tutorial as soon as possible.

Complex numbers: Lecture 6

We learnt 3 important things in today's lecture.
1. Geometrical interpretation of multiplication/division of complex numbers
2. Loci in the form of |z-a|=r
3. Loci in the form of |z-a|=|z-b|

1. Geometrical interpretation of multiplication/division of complex numbers

• Multiplying a complex number z by i is equivalent of rotating z anti-clockwise about the origin by pi/2
• Multiplying a complex number z by -1 is equivalent of rotating z anti-clockwise about the origin by pi
• In general, multiplying a complex number z by another complex number with modulus k and argument x is equivalent of rotating z anti-clockwise about the origin by x and scale z by a factor of k.

2. Loci in the form of |z-a|=r

• Locus of |z-a|=r means the collection of all points that satisfy the equation, i.e. all the points whose distance to complex number a is r.
• Points with fixed distance to a given point a forms a circle with center at a and radius r.
• If the equation is changed to an inequality |z-a|>r or |z-a|< r, it means all the points whose distance to a is greater or smaller than r, which is the region outside or the interior region of the circle.

3. Loci in the form of |z-a|=|z-b|

• Locus of |z-a|=|z-b| means the collection of all points that satisfy the equation, i.e. all the points whose distances to a and b are equal.
• Points with equal distances to two fixed points a and b forms the perpendicular bisector of the line ab.
• If the equation is changed to an inequality |z-a|<|z-b|,it means all the points whose distance to a is smaller than the distance to b, which is the region on one side of the perpendicular bisector that is closer to a.
• If the equation is changed to an inequality |z-a|>|z-b|, it means all the points whose distance to a is greater than the distance to b, which is the region on one side of the perpendicular bisector that is closer to b.

Remark: when you draw the loci of an inequality, take note of whether the equal sign is included. If the circle or the perpendicular bisector itself are not included, you have to use dotted line.

After today's lecture, you can do the whole tutorial 10b and Q1,2, 4, 6, 8 and 9 in tutorial 10c.

Complex Numbers: Lecture 5

In this lecture, there are two main concepts.

1. Exponential form of a complex number
2. De Moivre's Theorem

Exponential form

You have already learnt the polar form of a complex number, i.e. \[z=r(cos\theta+i sin\theta)\]

By using the Euler's Equation: \[e^{i\theta}=cos\theta+i sin\theta\]
We can change polar form to exponential form \[z=re^{i\theta}\]

The laws of exponents for real numbers still hold for complex numbers. Hence, when complex numbers are written in exponential form, it is comparatively easy to do the computation.

De Moivre's Theorem

Basically De Moivre's Theorem tells us that \[(cos\theta+i sin\theta)^{n}=cos n\theta+i sin n\theta\] for all n being rational numbers.

It is directly derived from the exponential form of complex numbers.

De Moivre's Theorem is very useful in terms of simplifying trigonometric calculation.

After today's lecture, you can do all the questions in tutorial 10b except Q13.

Complex Numbers: Lecture 4

There are mainly two learning points in this lecture.

1. How to make use of the property of modulus and argument
2. the polar form of complex numbers.


In general, the property of argument is similar to the laws of logarithms. The properties are very important. Make sure that you are familiar with them and do not get confused between the properties of modulus and argument.

For the polar form of complex number, \[z=r(sin\theta+icos\theta)\], where r is the modulus (distance from z to the origin in argand diagram) and \[\theta\] is the argument (angle between the complex number and the positive x-axis in argand diagram)

Given the polar form, you can get the cartesian form easily by calculating \[sin\theta\] and \[cos\theta\].

Given the cartesian form, if you want to get the polar form, find the modulus and the argument first.

After this lecture, you can attempt tutorial 10b Q1, Q3, Q5, Q6, Q7 and Q13

Complex Numbers: Lecture 3

In today's lecture, you learnt two important concepts of complex numbers: moduli and argument.

1. Moduli

• Modulus of a complex number z, denoted by z, represents the distance between z and origin in the argand diagram. Hence, we have

- |z| is non-negative

- |z|=0 if and only if z=0

• z1-z2 or z2-z1 represents the distance between z1 and z2 in the argand diagram.

2. Argument

• If z is represented by point P in the argand diagram, argument of z is the angle between OP and the positive real axis.
• The principal argument of z is in the interval (-pi, pi]. Take note that -pi is not included by pi is included! (why not include both?)
• To find the argument of z=x+yi

- find the basic angle using \[tan^{-1}\frac{y}{x}\]

(If you don't know what basic angle is, please revise your secondary school work.)

- determine which quadrant z lies in and use the basic angle to get the argument

3. Properties of argument and modulus

• Properties of argument is similar to the properties of logarithm. This is not by coincidence. After you learnt the exponential form of complex numbers, you will know the reason.

After today's lecture, you can attempt Q1 and Q3 in tutorial 10b.

Complex Numbers: Lecture 2

In today's lecture, there are three main concepts.

1. Complex conjugates

• If z=x+yi, then its conjugate is x-yi, denoted by z*.
• z and z* are reflections along the x-axis.
• \[ \left |z|\right =\sqrt{x^{2}+y^{2}}\], where z is called the modulus of z. (You can think of z as a vector in the argand diagram. Do you still remember the modulus of a vector?)
• \[ zz^{*}=z^{2} \]

The seven properties of the complex conjugates are very important. Please make use that you learn them by heart.

2. Division of complex numbers

• to calculate z1/z2, multiply it by z2*/z2* ( similar to how you rationalize the denominator when it is surds)
• While you are doing the computation, always remind yourself that \[i^{2}=-1\]

3. Polynomial equations with real coefficients.

• For a polynomial equations with real coefficients, if z is a root, then z* is also a root.

If you want to know more about this theorem, you can refer to http://en.wikipedia.org/wiki/Complex_conjugate_root_theorem

By now you should be able to do the whole tutorial 10a.

Complex Numbers: Lecture 1

Computation of complex numbers

• \[i^{2}=-1\]
• Real number is a subset of complex number.
• The representation of a complex number, z=x+yi is known as the cartesian form.
• Learn how to add, subtract and multiply two complex numbers
• Learn how to find the square root of a complex number.

Argand diagram

• We use the number line to represent real number, which is one dimensional. We use a plane to represent complex numbers, which has both real and imaginary part and hence two dimensional.
• Every complex number corresponds to a point on the plane and hence correspond to the position vector of that point.

Complex Numbers: Why do we need them?

I guess a lot of you are wondering why we need complex number. Can't we do with just real numbers? The following are videos that explain why we need complex numbers. I find it pretty good. =)


Part 1
http://www.youtube.com/watch?v=BDIv7r-X2kk


Part 2
http://www.youtube.com/watch?v=rBOzwh5-iGc&feature=related

Functions: Lecture 3

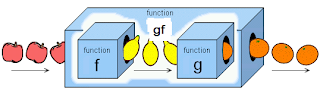The diagram is a good illustration of a composite function.

1. A set of values (Domain of f, apples in the diagram) are imput in the the f function box and the output will be the range of f.

2. The output from f (the lemon in the diagram) is again input into the g funtion box and the outcome will the range of this composite function gf.

3. Imagine that if some of the lemons out from f are too big to fit into g, then the composite machine will fail. Hence, we say that the range of f must be a subset of (including equal to) the domain of g for the composite function to exist.

Hence for composite function, there are a few points to take note of :

• The domain of gf is the domain of f.
• For gf to exist, range of f must be a subset of (including equal to) the domain of g.
• If gf does not exist, in order to make it exist, we have to narrow down the range of f (so as to make it a subset (or equal to) of the domain of g), and hence we need to narrow down the domain of f.
• The largest possible range of f that we can take is equal to the domain of g. Based on this largest possible range of f, we can find the corresponding largest possible domain of f.

Remark: Graph will be very useful in terms of finding range and domain!

Now you can do all the tutorial questions.

Functions: Lecture 2

One to One Function

• A function is one-to-one if no two elements in X are mapped to the same values.
• You can use a horizontal line test to check whether a function is one-to-one.

Inverse Function

• A function has inverse if and only if it is one-to-one. (Why?)
• The domain of function f is the range of its inverse. The range of function f is the domain of its inverse. (Why?)
• The graph of a function and its inverse are the reflections of each other along the line y=x (Why?)
• To find the value for which \[f(x)=f^{-1}(x)\], you need to find the intersection between the graph y=f(x) and y=x using G.C. (Why?)

Inverse Trigonometry Functions

• To ensure sin, cosine and tangent functions have inverse, we have to define principle range (restrict their domains)
• Principal range of sin inverse is [ -pi/2, pi/2]
• Principal range of cos inverse is [0, pi]
• Principal range of tan inverse is [-pi/2, pi/2]

G.C.

When you plot the graph of a function in G.C., do you know how to input the domain like (-1,1)

Ans: You input x>-1 and x<1>"and" can be found in 2nd -> Math -> Logic

Tutorial Questions to attempt

You can attend Q2 to Q5 after today's lecture.

Function: Lecture 1

By the end of the lecture, you are supposed to know the followings:

1. What is a function?

• Can you give a definition?
• Given a graph or an expression, do you know how to check whether it is a function?
• How do you know whether two functions are identical?

2. What are the domain and range of a function?Given a function, how can you find out the domain and the range?
3. What is a restriction of a function?
4. What is maximal domain and how to find out the maximal domain given the function?

Some learning points in this lecture

Notations:

[a, b] This is usually called a closed interval since both the end points a and b are included in the range.

(a, b) This is usually called an open interval since both the end points a and b are NOT included in the range.

[a, b) and (a, b] These two are called half-open-half-closed intervals.

Remark: If one end of the interval goes to infinity (either positive or negative), that end is always denoted with the open bracket ")" or "("

\[D_{f}\] denotes the domain of function f

\[R_{f}\] denotes the range of function f


Concepts

1. A function maps one element in X to one and ONLY one element in Y. But two different elements in X are allowed to be mapped to the same element in Y.
(Think about this point carefully! Can you give an example of the functions that map two different values of X to the same value of Y?)

2. Based on point 1, we can have vertical line test to check whether a graph is a function.

• If any vertical line cut the graph at only one point, it is a function. (one value of X to only one value of Y)
• If there exists a vertical line cutting the graph at more than one point, it is not a function. (one value of X to many values of Y)

3. Two functions are the same if and only if they have both the same rule and domain.

4. If the domain of a function is not specified, it is taken to be the maximal domain for which the function is defined, i.e. x takes whatever values that it is allowed to take.

G.C Skills

How to graph a function with the domain?

Remark: You have to take note of the END POINT in the graph to see whether it is included. The range can be read from the graph.

Tutorial question to attepmt

You can attempt Tutorial Q1 after today's lecture.

An Interesting function

In A level, you usually see functions that are very nice. Have you ever thought of a function like this:
\[f(x)=\left\{\begin{matrix}1 & \mbox{if x is rational}\\ 0 & \mbox{if x is irrational}\end{matrix}\right.\]

If you want to draw a graph of the function, remember that
1. Between every pair of irrational numbers, there is a rational number.
2. Between every pair of rational numbers, there is a irrational number.

Have you thought of how to integrate such a function? Does it have an area between the graph and the x-axis?

The answer to the question reveals a very important relationship between the rational and irrational numbers.

Let's start the MATH journey 2010!

Hi all,

This is a blog to assist you in the learning of H2 math in 2010. The content of this blog includes the following:

1. A summary for the lecture after each lecture.

2. The tutorial questions that you can attempt after each lecture.

3. interesting historical stories or video regarding the topics that you are learning

You are welcome to ask questions in the comments. I will answer them during the tutorial.

This blog is intended to help you to become more independent and active in the learning process. I hope you will make full use of it.

Sincerely hope that the case in the picture won't happen in my class =P